I diagrammi di Eulero-Venn: una rappresentazione grafica degli insiemi

I diagrammi di Eulero-Venn, spesso semplicemente chiamati “diagrammi di Venn“, sono strumenti grafici essenziali nella teoria degli insiemi, un ramo fondamentale della matematica. Questi diagrammi offrono una rappresentazione visiva che facilita la comprensione delle relazioni tra insiemi differenti, rendendo concetti complessi più accessibili e intuitivi. Il loro utilizzo spazia dall’analisi logica alla statistica, dall’informatica alla biologia. Vediamo in dettaglio cosa sono, come si usano, e perché sono così importanti.
Storia e origini
I diagrammi di Venn devono il loro nome al matematico britannico John Venn, che li introdusse nel 1880. Tuttavia, rappresentazioni grafiche di relazioni tra insiemi erano già in uso precedentemente, come nei lavori di Leonhard Euler, un matematico del XVIII secolo. La differenza sostanziale tra i diagrammi di Eulero e quelli di Venn consiste nel fatto che i primi possono omettere alcune parti di insiemi vuoti, mentre i secondi rappresentano tutti i possibili incroci, anche se vuoti.
Definizione e caratteristiche
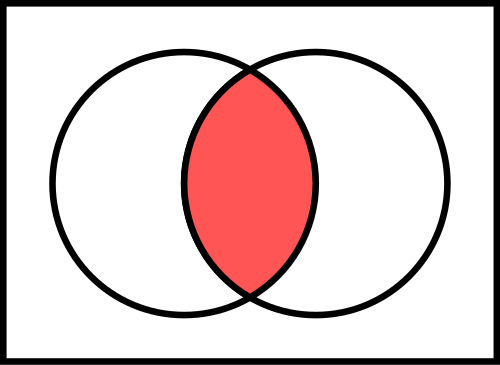
Un diagramma di Venn rappresenta insiemi attraverso cerchi (o altre forme chiuse) che si sovrappongono parzialmente o totalmente. Ogni cerchio rappresenta un insieme, e le aree di sovrapposizione tra i cerchi rappresentano gli elementi comuni a più insiemi.
In sintesi, i punti principali da notare includono:
- rappresentazione degli insiemi: ogni cerchio rappresenta un insieme distinto;
- intersezioni: le aree di sovrapposizione gli elementi in comune tra gli insiemi;
- universalità: un diagramma di Venn di n insiemi rappresenta, attraverso il rettangolo esteriore, tutte le possibili intersezioni tra questi insiemi, incluso l’insieme vuoto.
Esempio
Qualora dovessimo rappresentare attraverso un diagramma di Eulero-Venn gli insiemi K {a, b, c, d} e L {c, d, e, f}, noteremo subito che possiedono degli elementi in comune. Il grafico che pertanto otterremo sarà il seguente:
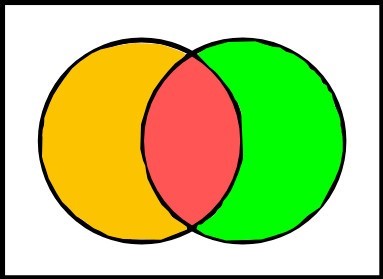
In questo caso la parte arancione rappresenta l’insieme K, con gli elementi a, b, la parte verde indica l’insieme L, con gli elementi e, f. La parte rossa invece contiene gli elementi in comune dei due insiemi, detta anche intersezione. Essa conterrà gli elementi c, d. Quindi si rappresenterà: K∩L = {c, d}.
Applicazioni quotidiane
- teoria degli insiemi: i diagrammi di Venn sono utilizzati per illustrare le operazioni tra insiemi, come l’intersezione, l’unione e la differenza, tutti argomenti di cui parleremo nei prossimi articoli che ti invito a non perdere;
- logica e matematica: aiutano a visualizzare e risolvere problemi logici e probabilistici;
- statistica: sono utili per rappresentare la probabilità di eventi combinati;
- informatica: sono usati nei linguaggi di programmazione per illustrare operazioni booleane;
- biologia e scienze: aiutano a rappresentare relazioni tra diverse specie o categorie.






